Philosophy
Made from aluminum, bambo, cardboard, plastic, or "gerroplast" [polystyrene foam] the ole "slide rule" still garners interest...a definite indicator of one's course studies in college and an icon of the professional scientist...and it wasn't a bad babe magnet either. It also beat fussing with five place logarithm tables using paper and pencil. But now, it is relegated to historians of scientific instruments and general collectors. Some do fetch premium prices.
William Oughtred
1575-166
English mathematician, born at Eton, and educated there and at King's College, Cambridge, of which he became fellow. Being admitted to holy orders, he left the university about 1603, and was presented to the rectory of Aldbury, near Guildford in Surrey; and about 1628 he was appointed by the earl of Arundel to instruct his son in mathematics. He corresponded with some of the most eminent scholars of his time on mathematical subjects; and his house was generally full of pupils from all quarters. It is said that he expired in a sudden transport of joy upon hearing the news of the vote at Westminster for the restoration of Carles II. He published, among other mathematical works, Clavis Mathematica, in 1631, in which he introduced new signs for certain mathematical operations; a treatise on navigation entitled Circles of Proportion, in 1632; works on trigonometry and dialling, and his Opuscula Mathematica, published posthumously in 1676. He is best known for having invented the slide rule (1622), his name being taken by the organization of slide-rule collectors, the Oughtred Society.
Clavis Mathematicae [1631]
Circles of Proportion and the Horizontal Instrument [1632]
Trigonometria [1657]
Opuscula Mathematica Hactenus Inedita [1677]
A brief history...
In 1677, Henry Coggeshall created a two-foot folding rule for timber measure, called the Coggeshall slide rule. His design and uses for the tool gave the slide rule purpose outside of mathematical inquiry.
In 1722, Warner introduced the two- and three-decade scales, and in 1755 Everard included an inverted scale; a slide rule containing all of these scales is usually known as a "polyphase" rule.
In 1815, Peter Roget invented the log log slide rule, which included a scale displaying the logarithm of the logarithm. This allowed the user to directly perform calculations involving roots and exponents. This was especially useful for fractional powers.
The more modern form was created in 1859 by French artillery lieutenant Amédée Mannheim, "who was fortunate in having his rule made by a firm of national reputation and in having it adopted by the French Artillery." It was around that time, as engineering became a recognized professional activity, that slide rules came into wide use in Europe. They did not become common in the United States until 1881, when Edwin Thacher introduced a cylindrical rule there. The duplex rule was invented by William Cox in 1891, and was produced by Keuffel and Esser Co. of New York.
Astronomical work also required fine computations, and in 19th century Germany a steel slide rule about 2 meters long was used at one observatory. It had a microscope attached, giving it accuracy to six decimal places.
In World War II, bombardiers and navigators who required quick calculations often used specialized slide rules. One office of the U.S. Navy actually designed a generic slide rule "chassis" with an aluminum body and plastic cursor into which celluloid cards (printed on both sides) could be placed for special calculations. The process was invented to calculate range, fuel use and altitude for aircraft, and then adapted to many other purposes. The E6-B Flight Computer, a circular sliderule with added features is still used today in aviation, particularly by student pilots.
Throughout the 1950s and 1960s the slide rule was the symbol of the engineer's profession (in the same way that the stethoscope symbolized the medical profession). As an anecdote it can be mentioned that German rocket scientist Wernher von Braun brought two 1930s vintage Nestler slide rules with him when he moved to the U.S. after World War II to work on the American space program. Throughout his life he never used any other pocket calculating devices; slide rules obviously served him perfectly well for making quick estimates of rocket design parameters and other figures. Aluminum Pickett-brand slide rules were carried on five Apollo space missions, including to the moon, according to advertising on Pickett's N600 slide rule boxes.--Wikipedia.
From The Museum of HP Calculators:
Basic Slide Rule Instructions:
To multiply two numbers on a typical slide rule, the user set the left index (start of the scale) on the C scale to line up with one factor on the D scale. (All labels refer to Pickett scales. Scale labels were not completely uniform between brands.) The user then found the second factor on the C scale and looked on the D scale for the product. By doing this, the user effectively added the logs (lengths) of the two numbers and looked up the antilog.
Multiplications with more than a single digit were carried out by making use of the smaller graduations to represent additional digits of decreasing significance. The precision available to the user was directly proportional to the size of the device (or the smallest lines the user could resolve.) The slide rule did not indicate the decimal point. That was done by the user - typically by estimation, "common sense" or by computing the characteristic. For example:
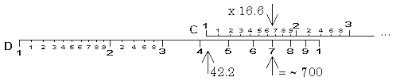Here the result is 7 - estimation of 10x40 and 20x40 makes it obvious that the result is 700. (The 41' cylindrical Fuller model makes it clear that the result is just above 700.5.)
Division was performed by reversing the multiplication steps (setting the divisor on the C scale opposite the dividend on the D scale and reading the result of the D scale under the C scale index.) To multiply multiple numbers, the user simply moved the C index to the previous product to start the next multiplication. (The hairline was handy for keeping a pointer on the previous product while moving the slide.)
There were many other scales. Many were for unary functions which required no sliding. Some common scales were:
CI and DI: Reciprocals:
These scales were the reciprocal (1/x) of C and D respectively. The user found the number on C or D and read the reciprocal on CI or DI respectively. For example, placing the hairline on 2 on the C scale, the user could read the reciprocal of 5 (.5) on the CI scale. Of course, the process is reversible since .2 is the reciprocal of 5. There were two scales for convenience.
CF, DF, CIF and DIF: Folded Scales:
These scales were "folded" such that instead of having 1 at each end and Pi in the middle, they started at Pi, ran up to 1 in the middle, and then went from 1 to Pi again on the other end. These scales were used to avoid resetting the slide when a problem would otherwise go off the end. For example, if after aligning the index of C with the first factor on D, the second factor on C was off scale, then the user could instead find the second factor on CF and read the result on DF.
A and B: Square/Square Root:
These were the squares of the D and C scales respectively. To determine a square root, the user found the number on A and read the root on D. The process was reversed to find a square. The A scale was simply a D scale, reduced to half its length and printed twice. (The magic of logarithms again.)
As with C and D, there was one fixed and one moving square scale. This allowed a square or square root to be easily included in a chained or combined calculation. (eg. multiplying by the square or square root of a number could be done in a single operation.)
The tricky part was determining which side of the A scale to use. For example, the square root of 1.44 is 1.2 and the square root of 144 is 12 - both of which could be correctly read from the left side of the A scale. However, the user needed to read the square root of 14.4 from the right side of the scale to get the correct answer of ~3.8. The simplest trick was to write the number in standard form (ie n.nnn x 10^exp) and use the left side for even powers of 10. (And the resulting exponent was one half the original exponent.) For odd powers of ten, the user shifted the decimal one place to the right and decreased the exponent of ten by one. Then the user used the right side (and again used one half the exponent of ten for the resulting exponent.)
R1 and R2: Square/Square Root:
Whereas A and B were the squares of C and D, some rules also added R1 and R2 which were the square root of D. Instead of 2 D scales reduced to half size, the R1 scale was one half a D scale doubled in size and the R2 scale was the second half. This allowed significantly greater precession.
K: Cube/Cube Root:
This scale was used for cubes or cube roots. To find a cube root, the user found the number on K and read the cube root on D. The K scale was simply a D scale shrunk and repeated three times - and the user needed to correctly decide which of the three scales to use for any number. This process was similar to the process used on the squaring scales.
L: Common Logarithms:
This scale was used to determine the log (base 10) of a number. More precisely, it determined the mantissa of the logarithm and the user determined the characteristic. For example, placing the hairline on the 2 on the D scale, and reading from the L scale showed that the mantissa of the log of 2 is .3. So the log of 2 is .3, the log of 20 is 1.3, the log of 200 is 2.3 etc. The user also had to remember that when the number was small, the characteristic became negative but the mantissa remained positive. So to compute the log of .2, the user added -1 to .3 and the result was -0.7. (The process was reversed for antilogs.)
Since this scale was used to read the values of logs, it was not written in log scale but instead had the values 0 - 1 evenly spaced. It was the D scale that was logarithmic. In fact the L scale was the only non-logarithmic scale that was commonly found on slide rules.
S: Sines and Cosines:
Since the sin x = cos(90-x) the same scale was easily used for both sines and cosines. (The angles for both the cosine and sine were typically printed.) The user read the angle of the sine or cosine on the S scale (keeping in mind that sines increased to the left) and read the result from the D scale.
Cos S: Sines and Cosines:
A common alternate labeling for the S scale. (See above.)
T: Tangents and Cotangents:
The T scale was used with C or CI to find tangents and cotangents. Again, only one scale was needed since tan x = cot(90-x). Also, since tan x = 1/cot x, a single position on the T scale could be read as a tangent or cotangent by looking at C or CI.
ST: Sines and Tangents for Small Angles:
A single scale for finding sines and tangents for small angles - typically less than 5.7 degrees. Since sines and tangents are very close in this region, a single scale was used for both.
Log-log Slide Rules:
Log-log rules were invented in 1815 and had scales proportional to the log of the log of the number. This allowed the user to calculate X^Y in a fashion similar to that used for multiplication. (See above.) Log-log rules can be recognized by the many scales starting with "LL".
Unlike the multiplication scales, the log-log scales did not require the user to determine the decimal point. The scales represented a fairly large range of numbers typically from 0.000045 to 22,000.
To raise a number greater than 1.001 to a power, the LL0 - LL3 scales were used. The four scales represented a continuous range of numbers typically from 1.001 at the left end of LL0 to about 22,000 at the right end of LL3. To raise the number X to the power Y, the index of C was set to line up with the number X on whichever LL scale X appeared on. (Again note that the LL scales were not floating point.) Then the user found Y on the C scale and read the result on the same LL scale. Reading the result on the next higher labeled scale would indicate X^(Y*10). Reading the result on the next lower labeled scale would indicate X^(Y/10) and so on.
For example, setting the index of C to align with 1.4 on LL2 and the hairline on 2 of C, the user could read that 1.4^2 is 1.96 on LL2, 1.4^20 is ~840 on LL3, 1.4^.2 is 1.0696 on LL1, and 1.4^.02 is 1.00675 on LL0. (All of these results were read on a 10" rule.) To raise a number less than .999 to a power, the LL/0 - LL/3 scales were used.
Dietzgen/Gilson Midget Circular Slide Rule
Hughes Owens Co. Ltd 1760 [1952]
Merc's Slide Rule
Places to visit...
- Cheating And Breaking The Rules
Professional golf has made a certain kind of club illegal. It disallows certain kinds of grooves on the head that add spin to the shot, allowing players to cover up what would have been a bad spot with the extra spin. As the rule is written, there happen...
- Just How Small Is An Atom?
When it comes to the world beyond our direct, ordinary experience, we just don't have what it takes to understand the differences in scale. If you are given a model Earth and Moon made to scale, for instance, and you're asked to estimate how far...
- My Trip Out West
I think I've spent my life on the East Coast, and as far as I can remember, just about every state I've ever visited has had direct access to the Atlantic Ocean. A few weeks ago, however, I went on a little vacation out west and visited some amazing...
- Anders Celsius...the Swedish Thermometer...fahrenheit's Scientific Buddy
Anders Celsius Novemebr 27th, 1701 to April 25th, 1744 Swedish astronomer, physicist and mathematician who is famous for the temperature scale he developed. Celsius was born in Uppsala where he succeeded his father as professor of astronomy in 1730....
- March 3rd, 2009--3/3/09--√9 = 3--3² = 3 × 3 = 9
Nearly slipped by...this is "Square Root Day" celebrated by math aficionados. It is a rare mathematical function event that won't happen again until April 4th, 2016. Tuesday is "Square Root Day", a holiday that occurs when the day and the month are...
Philosophy
Sliderules
Made from aluminum, bambo, cardboard, plastic, or "gerroplast" [polystyrene foam] the ole "slide rule" still garners interest...a definite indicator of one's course studies in college and an icon of the professional scientist...and it wasn't a bad babe magnet either. It also beat fussing with five place logarithm tables using paper and pencil. But now, it is relegated to historians of scientific instruments and general collectors. Some do fetch premium prices.Father of the sliderule...
William Oughtred1575-166
English mathematician, born at Eton, and educated there and at King's College, Cambridge, of which he became fellow. Being admitted to holy orders, he left the university about 1603, and was presented to the rectory of Aldbury, near Guildford in Surrey; and about 1628 he was appointed by the earl of Arundel to instruct his son in mathematics. He corresponded with some of the most eminent scholars of his time on mathematical subjects; and his house was generally full of pupils from all quarters. It is said that he expired in a sudden transport of joy upon hearing the news of the vote at Westminster for the restoration of Carles II. He published, among other mathematical works, Clavis Mathematica, in 1631, in which he introduced new signs for certain mathematical operations; a treatise on navigation entitled Circles of Proportion, in 1632; works on trigonometry and dialling, and his Opuscula Mathematica, published posthumously in 1676. He is best known for having invented the slide rule (1622), his name being taken by the organization of slide-rule collectors, the Oughtred Society.
Clavis Mathematicae [1631]
Circles of Proportion and the Horizontal Instrument [1632]
Trigonometria [1657]
Opuscula Mathematica Hactenus Inedita [1677]
A brief history...
In 1677, Henry Coggeshall created a two-foot folding rule for timber measure, called the Coggeshall slide rule. His design and uses for the tool gave the slide rule purpose outside of mathematical inquiry.
In 1722, Warner introduced the two- and three-decade scales, and in 1755 Everard included an inverted scale; a slide rule containing all of these scales is usually known as a "polyphase" rule.
In 1815, Peter Roget invented the log log slide rule, which included a scale displaying the logarithm of the logarithm. This allowed the user to directly perform calculations involving roots and exponents. This was especially useful for fractional powers.
The more modern form was created in 1859 by French artillery lieutenant Amédée Mannheim, "who was fortunate in having his rule made by a firm of national reputation and in having it adopted by the French Artillery." It was around that time, as engineering became a recognized professional activity, that slide rules came into wide use in Europe. They did not become common in the United States until 1881, when Edwin Thacher introduced a cylindrical rule there. The duplex rule was invented by William Cox in 1891, and was produced by Keuffel and Esser Co. of New York.
Astronomical work also required fine computations, and in 19th century Germany a steel slide rule about 2 meters long was used at one observatory. It had a microscope attached, giving it accuracy to six decimal places.
In World War II, bombardiers and navigators who required quick calculations often used specialized slide rules. One office of the U.S. Navy actually designed a generic slide rule "chassis" with an aluminum body and plastic cursor into which celluloid cards (printed on both sides) could be placed for special calculations. The process was invented to calculate range, fuel use and altitude for aircraft, and then adapted to many other purposes. The E6-B Flight Computer, a circular sliderule with added features is still used today in aviation, particularly by student pilots.
Throughout the 1950s and 1960s the slide rule was the symbol of the engineer's profession (in the same way that the stethoscope symbolized the medical profession). As an anecdote it can be mentioned that German rocket scientist Wernher von Braun brought two 1930s vintage Nestler slide rules with him when he moved to the U.S. after World War II to work on the American space program. Throughout his life he never used any other pocket calculating devices; slide rules obviously served him perfectly well for making quick estimates of rocket design parameters and other figures. Aluminum Pickett-brand slide rules were carried on five Apollo space missions, including to the moon, according to advertising on Pickett's N600 slide rule boxes.--Wikipedia.
From The Museum of HP Calculators:
Basic Slide Rule Instructions:
To multiply two numbers on a typical slide rule, the user set the left index (start of the scale) on the C scale to line up with one factor on the D scale. (All labels refer to Pickett scales. Scale labels were not completely uniform between brands.) The user then found the second factor on the C scale and looked on the D scale for the product. By doing this, the user effectively added the logs (lengths) of the two numbers and looked up the antilog.
Multiplications with more than a single digit were carried out by making use of the smaller graduations to represent additional digits of decreasing significance. The precision available to the user was directly proportional to the size of the device (or the smallest lines the user could resolve.) The slide rule did not indicate the decimal point. That was done by the user - typically by estimation, "common sense" or by computing the characteristic. For example:
Here the result is 7 - estimation of 10x40 and 20x40 makes it obvious that the result is 700. (The 41' cylindrical Fuller model makes it clear that the result is just above 700.5.)Division was performed by reversing the multiplication steps (setting the divisor on the C scale opposite the dividend on the D scale and reading the result of the D scale under the C scale index.) To multiply multiple numbers, the user simply moved the C index to the previous product to start the next multiplication. (The hairline was handy for keeping a pointer on the previous product while moving the slide.)
There were many other scales. Many were for unary functions which required no sliding. Some common scales were:
CI and DI: Reciprocals:
These scales were the reciprocal (1/x) of C and D respectively. The user found the number on C or D and read the reciprocal on CI or DI respectively. For example, placing the hairline on 2 on the C scale, the user could read the reciprocal of 5 (.5) on the CI scale. Of course, the process is reversible since .2 is the reciprocal of 5. There were two scales for convenience.
CF, DF, CIF and DIF: Folded Scales:
These scales were "folded" such that instead of having 1 at each end and Pi in the middle, they started at Pi, ran up to 1 in the middle, and then went from 1 to Pi again on the other end. These scales were used to avoid resetting the slide when a problem would otherwise go off the end. For example, if after aligning the index of C with the first factor on D, the second factor on C was off scale, then the user could instead find the second factor on CF and read the result on DF.
A and B: Square/Square Root:
These were the squares of the D and C scales respectively. To determine a square root, the user found the number on A and read the root on D. The process was reversed to find a square. The A scale was simply a D scale, reduced to half its length and printed twice. (The magic of logarithms again.)
As with C and D, there was one fixed and one moving square scale. This allowed a square or square root to be easily included in a chained or combined calculation. (eg. multiplying by the square or square root of a number could be done in a single operation.)
The tricky part was determining which side of the A scale to use. For example, the square root of 1.44 is 1.2 and the square root of 144 is 12 - both of which could be correctly read from the left side of the A scale. However, the user needed to read the square root of 14.4 from the right side of the scale to get the correct answer of ~3.8. The simplest trick was to write the number in standard form (ie n.nnn x 10^exp) and use the left side for even powers of 10. (And the resulting exponent was one half the original exponent.) For odd powers of ten, the user shifted the decimal one place to the right and decreased the exponent of ten by one. Then the user used the right side (and again used one half the exponent of ten for the resulting exponent.)
R1 and R2: Square/Square Root:
Whereas A and B were the squares of C and D, some rules also added R1 and R2 which were the square root of D. Instead of 2 D scales reduced to half size, the R1 scale was one half a D scale doubled in size and the R2 scale was the second half. This allowed significantly greater precession.
K: Cube/Cube Root:
This scale was used for cubes or cube roots. To find a cube root, the user found the number on K and read the cube root on D. The K scale was simply a D scale shrunk and repeated three times - and the user needed to correctly decide which of the three scales to use for any number. This process was similar to the process used on the squaring scales.
L: Common Logarithms:
This scale was used to determine the log (base 10) of a number. More precisely, it determined the mantissa of the logarithm and the user determined the characteristic. For example, placing the hairline on the 2 on the D scale, and reading from the L scale showed that the mantissa of the log of 2 is .3. So the log of 2 is .3, the log of 20 is 1.3, the log of 200 is 2.3 etc. The user also had to remember that when the number was small, the characteristic became negative but the mantissa remained positive. So to compute the log of .2, the user added -1 to .3 and the result was -0.7. (The process was reversed for antilogs.)
Since this scale was used to read the values of logs, it was not written in log scale but instead had the values 0 - 1 evenly spaced. It was the D scale that was logarithmic. In fact the L scale was the only non-logarithmic scale that was commonly found on slide rules.
S: Sines and Cosines:
Since the sin x = cos(90-x) the same scale was easily used for both sines and cosines. (The angles for both the cosine and sine were typically printed.) The user read the angle of the sine or cosine on the S scale (keeping in mind that sines increased to the left) and read the result from the D scale.
Cos S: Sines and Cosines:
A common alternate labeling for the S scale. (See above.)
T: Tangents and Cotangents:
The T scale was used with C or CI to find tangents and cotangents. Again, only one scale was needed since tan x = cot(90-x). Also, since tan x = 1/cot x, a single position on the T scale could be read as a tangent or cotangent by looking at C or CI.
ST: Sines and Tangents for Small Angles:
A single scale for finding sines and tangents for small angles - typically less than 5.7 degrees. Since sines and tangents are very close in this region, a single scale was used for both.
Log-log Slide Rules:
Log-log rules were invented in 1815 and had scales proportional to the log of the log of the number. This allowed the user to calculate X^Y in a fashion similar to that used for multiplication. (See above.) Log-log rules can be recognized by the many scales starting with "LL".
Unlike the multiplication scales, the log-log scales did not require the user to determine the decimal point. The scales represented a fairly large range of numbers typically from 0.000045 to 22,000.
To raise a number greater than 1.001 to a power, the LL0 - LL3 scales were used. The four scales represented a continuous range of numbers typically from 1.001 at the left end of LL0 to about 22,000 at the right end of LL3. To raise the number X to the power Y, the index of C was set to line up with the number X on whichever LL scale X appeared on. (Again note that the LL scales were not floating point.) Then the user found Y on the C scale and read the result on the same LL scale. Reading the result on the next higher labeled scale would indicate X^(Y*10). Reading the result on the next lower labeled scale would indicate X^(Y/10) and so on.
For example, setting the index of C to align with 1.4 on LL2 and the hairline on 2 of C, the user could read that 1.4^2 is 1.96 on LL2, 1.4^20 is ~840 on LL3, 1.4^.2 is 1.0696 on LL1, and 1.4^.02 is 1.00675 on LL0. (All of these results were read on a 10" rule.) To raise a number less than .999 to a power, the LL/0 - LL/3 scales were used.
Various Instruments
Dietzgen/Gilson Midget Circular Slide RuleThe rule is a single piece of metal, with rotating cursors. Roughly, the long cursor corresponds to the slide, the short to the cursor on a straight rule. Most calculations are made by setting one cursor, then moving the other cursor, which causes both cursors to move in tandem, keeping the angle between them constant. The reverse side has only one cursor because it's trig functions and fractional equivalents, which only need the single cursor.
Bissaker's slide rule [bottom] is the earliest dated straight slide rule. The scales are mainly trigonometrical and logarithmic. The instrument is inscribed "Made by Robert Bissaker, 1654, for TW". Thacher's slide rule [top] is an extremely important American contribution to slide rules, capable of accurate reading to four decimal places.
Hughes Owens Co. Ltd 1760 [1952]It is only 4" long with the helpful magnifier.
Merc's Slide RuleTieclasp
Curiously, when my physicist uncle [Lawrence Howard Petersen Ph.D.] passed away, his tieclasp slide rule was buried with him.
Places to visit...
Dave's Slide Rule Gallery
My Slide Rule Collection
Slide Rules and Planimeters
The Slide Rule Trading Company
And finally, from "Themathguy" [Nate B.], make your own slide rule. Watch the video.
"Build yourself a slide rule"
- Cheating And Breaking The Rules
Professional golf has made a certain kind of club illegal. It disallows certain kinds of grooves on the head that add spin to the shot, allowing players to cover up what would have been a bad spot with the extra spin. As the rule is written, there happen...
- Just How Small Is An Atom?
When it comes to the world beyond our direct, ordinary experience, we just don't have what it takes to understand the differences in scale. If you are given a model Earth and Moon made to scale, for instance, and you're asked to estimate how far...
- My Trip Out West
I think I've spent my life on the East Coast, and as far as I can remember, just about every state I've ever visited has had direct access to the Atlantic Ocean. A few weeks ago, however, I went on a little vacation out west and visited some amazing...
- Anders Celsius...the Swedish Thermometer...fahrenheit's Scientific Buddy
Anders Celsius Novemebr 27th, 1701 to April 25th, 1744 Swedish astronomer, physicist and mathematician who is famous for the temperature scale he developed. Celsius was born in Uppsala where he succeeded his father as professor of astronomy in 1730....
- March 3rd, 2009--3/3/09--√9 = 3--3² = 3 × 3 = 9
Nearly slipped by...this is "Square Root Day" celebrated by math aficionados. It is a rare mathematical function event that won't happen again until April 4th, 2016. Tuesday is "Square Root Day", a holiday that occurs when the day and the month are...