The academics...future scholars

We are developing tools for designing nano-scale devices in which quantum degrees of freedom play an important role. Quantum systems with made-to-order properties, such as filters, modulators, and switches, are constructed from the atomic level up. The guiding idea of our approach is that in order to achieve such desired system responses, symmetries such as the translational invariance of conventional crystals have to be broken. The core of adaptive quantum design is therefore the search for optimum configurations of the system constituents, such as atomic positions in an artificial synthetic solid, that enable a desired system response, e.g. optical absorption at certain frequencies.

As an illustrative example, let us consider interacting atoms described by a long-ranged tight-binding model,

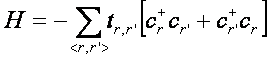
Here the overlap integral is determined by the distance between the atoms and by the nature of the atomic orbitals. The dependence on inter-atomic spacing can be parameterized as a power-law,

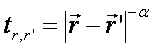
where α = 1.5 - 3.0. By breaking the translational symmetry of this system, desired responses can be emulated, e.g. a flat spectral function, or quasi-2D or quasi-3D response in a 1D array.

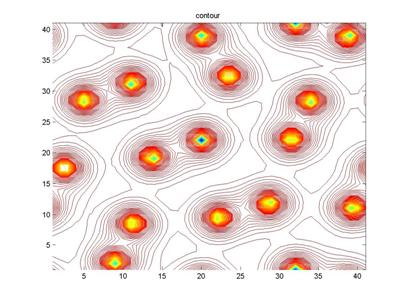
The above left figure shows the resulting spatial configuration of atoms in a two-dimensional system with periodic boundary conditions. The chosen target function in this case is a top-hat density of states that is flat within a certain energy regime, and zero otherwise (shown in the right figure). Since this specific target is particle-hole symmetric, i.e. there are as many states above and below zero-energy, the dominant building blocks that are discovered by the numerical search of the best system configuration are dimer molecules. Other target functions that break particle-hole symmetry require more complicated building blocks, such as trimer and quadrumer molecules.

Another example for adaptive quantum design are photonic structures with dielectric rods of variable size and position. Existing devices based on ordered photonic crystals have only limited functionality. On the other hand, adaptive design tools enable new optimized broken-symmetry nano-photonic devices with greater sensitivity, such as mux, combiners, splitters, and channel dropping filters.

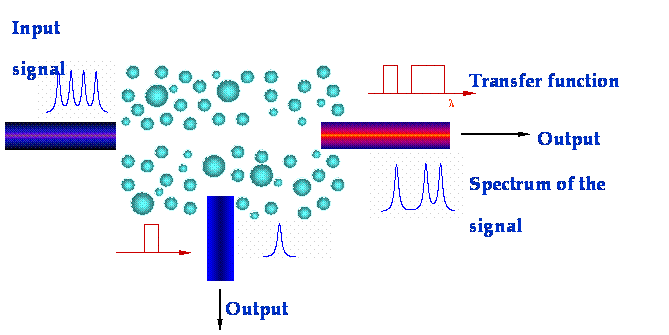
Effective numerical search algorithms are essential to find such configurations in the large phase space of possible solutions which includes collective many-body resonances. We have explored and tested several approaches, including guided random walk, simulated annealing, and genetic algorithms. Their convergence properties differ and depend strongly on system parameters. The plot below shows a comparison of these methods which were benchmarked on the same computer. The convergence criterion Δ in this case is the squared difference between a top-hat target density of states and the density of states achieved by adjusting the positions of the constituent atoms. Its is observed that some of the simpler search algorithms tend to get stuck in local minima, whereas the more sophisticated ones find a lower minimum.

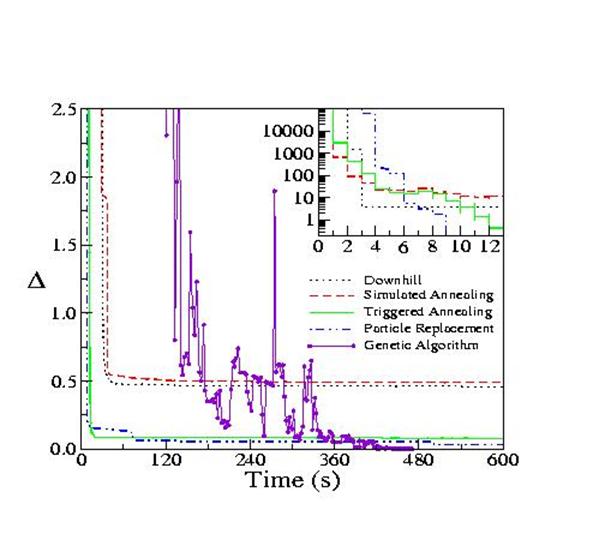
Adaptive quantum design is an enabling method for future advances in nano-technology. It relies on realistic physical models and on efficient numerical search algorithms for global minima. It can be applied to microscopic systems in order to enable and enhance their functionality. The challenge is to solve the inverse problem where a target solution is given and the corresponding system configuration has to be found. On the way to matching such target, new building blocks of broken-symmetry configurations can be discovered. This approach enables us to design ultra-small devices and simultaneously to discover novel phenomena that are not found in conventional solids.